fertvideos.blogg.se

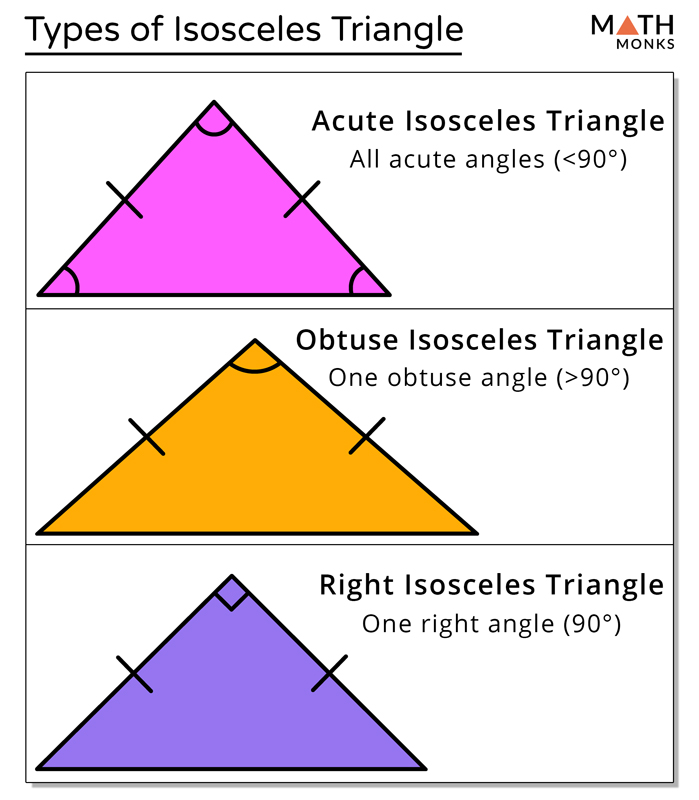
Furthermore, there can be at most one obtuse angle, and a right angle and an obtuse angle cannot occur in the same triangle. Proposition I.17 states that the sum of any two angles in a triangle is less than two right angles, therefore, no triangle can contain more than one right angle. Since triangle D has a right angle, it is a right triangle. An alternate characterization of isosceles triangles, namely that their base angles are equal, is demonstrated in propositions I.5 and I.6. It is only required that at least two sides be equal in order for a triangle to be isosceles.Įquilateral triangles are constructed in the very first proposition of the Elements, I.1. The way that the term isosceles triangle is used in the Elements does not exclude equilateral triangles. The term isosceles triangle is first used in proposition I.5 and later in Books II and IV. The equilateral triangle A not only has three bilateral symmetries, but also has 120°-rotational symmetries.Īccording to this definition, an equilateral triangle is not to be considered as an isosceles triangle. The scalene triangle C has no symmetries, but the isosceles triangle B has a bilateral symmetry. This definition classifies triangles by their symmetries, while definition 21 classifies them by the kinds of angles they contain. We find that ∠ABC, ∠CBD and ∠DBE make a straight angle.Further, of trilateral figures, a right-angled triangle is that which has a right angle, an obtuse-angled triangle that which has an obtuse angle, and an acute-angled triangle that which has its three angles acute. Solution: We can see that ABC is an isosceles triangle,

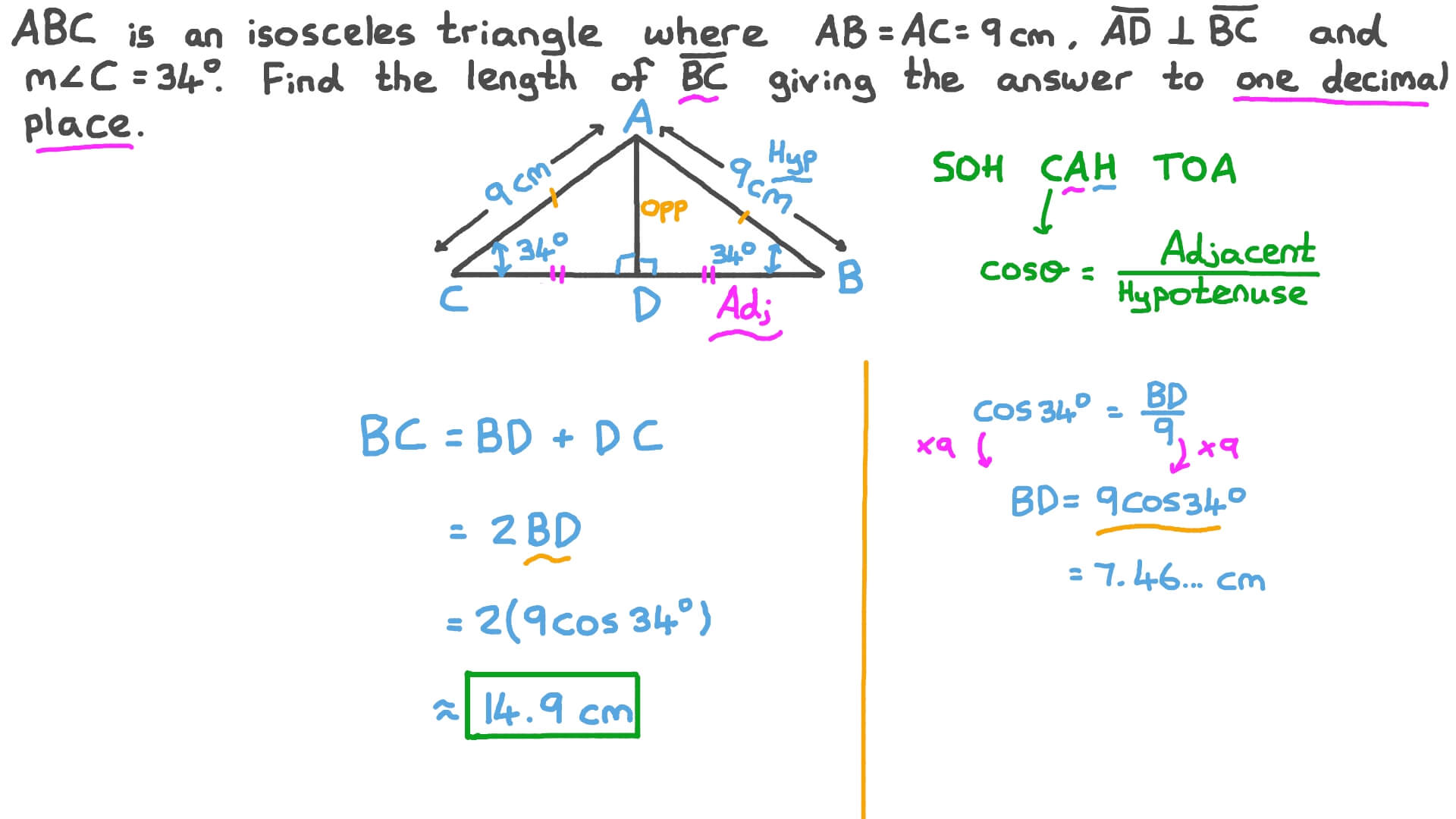
Problem 5: ABC and BCD are isosceles triangles. So, b is a length and therefore is positive where h = b - 4 = 6 ( b = 10), Now, solutions to the equation: b = 10 and b = - 6 Now, we need to substitute h by b - 4 in the formula for A

If one of the longer sides is 6.3 centimeters, which equation can be used to find the length of the base 6.3+b15.7 12.6+b15. The equation 2a + b 15.7 models this information. The perimeter of the triangle is 15.7 centimeters. Solution: We use the formula of area of the isosceles triangle This isosceles triangle has two sides of equal length, a, that are longer than the length of the base, b.

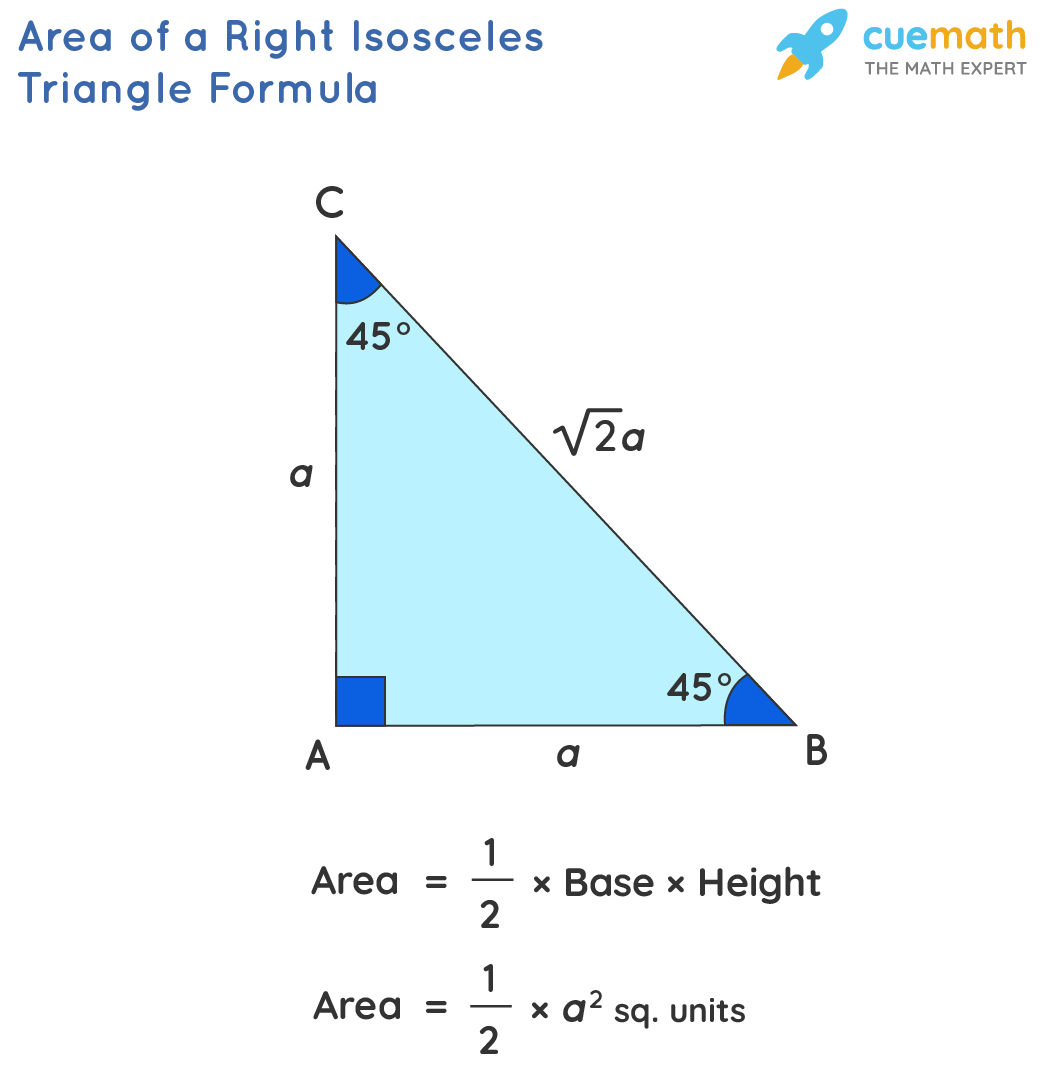
Problem 4: The height h (perpendicular to its base b) of the isosceles triangle is 4 cm shorter than its base b, and its area is 30 cm 2? What is the lateral side of it? Now, we use the formula of area of isosceles triangle Problem 3: An isosceles triangle has an area 20 unit with 2 and base 10 units. Problem 2: Find the perimeter of an isosceles triangle, with side 8 cm and base 6cm. Solution: Area of an isosceles triangle is ½ × b × h Problem 1: Determine the area of an isosceles triangle whose height is 9 cm and base as 6 cm? We will have a look at some of the solved questions to get some good idea. It is important to solve different problems related to the isosceles triangle. So, P = 2a + b where the two equal sides of the triangle is ‘a’ and the base of the triangle is ‘b’. It is through the knowledge of its base and side that the perimeter of an isosceles triangle can be found. We are familiar that the boundary of the shape is the perimeter of any shape. So A = ½ x b x h Isosceles Triangle Perimeter Formula The formula of an isosceles triangle is ½ x b x h where b and h are the base and height of the triangle respectively. The right-angled isosceles triangle has the third angle as 90 degrees.The measurement from the base to the vertex (topmost) of the triangle is the altitude of an isosceles triangle.The angles which are opposite to the two equal sides of the triangle are always equal.The two sides of an isosceles triangle are equal, whereas the base of the triangle is the unequal side.Based on the angles, the classification of the triangle is done in three types which are obtuse-angled, acute-angled and right-angled. An isosceles triangle is a triangle which has two of its three sides. A triangle is classified into three types based on the sides, namely isosceles, scalene and equilateral. sides equal and an equiangular polygon is a polygon with all its angles equal. It is based on the angles and sides when the classifications of the types of triangles are done. The opposite sides of the angles are equal. What is an Isosceles Triangle?Ī triangle that has any of its two sides equal to each other is called an isosceles triangle. Students would be able to work on the solved examples that would help to get the best idea about it. We would also concentrate on the isosceles triangle properties. Students would be able to learn about the area of an isosceles triangle as well as isosceles triangle formula. In this chapter, we will focus on the isosceles triangle.